Algunos matemáticos ven la belleza de las matemáticas en resultados que establecen conexiones entre dos áreas de las matemáticas que parecen distintas y sin relación alguna a primera vista. Estos resultados suelen ser llamados profundos. Aunque es muy dificil tener un acuerdo universal entre qué resultados son profundos, algunos ejemplos pueden ser citados. Uno de ellos es la Identidad de Euler:
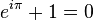
Richard Feyman la llama la fórmula más importante en las matemáticas. Ejemplos modernos pueden incluir el Teorema de la Modularidad, que establece una conexión importante entre las curvas elípticas y formas modulares.
Lo contrario a profundo, es trivial. Un teorema trivial puede ser un resultado que derive en una manera obvia y sencilla a comparación de otras formas para obtener resultados. Sin embargo, en ocasiones, el establecimiento de un teorema puede ser tan original que puede ser considerado como profundo, aunque su demostración sea obvia.
G.H. Hardy, en "A Mathematician's Apology", sugiere que la belleza matemática surge de un elemento sorpresa. Sin embargo, Gian-Carlo Rota está en desacuerdo con ello y propone un contraargumento:
"Un gran número de teoremas matemáticos, cuando fueron apenas publicados, parecen ser sorprendentes; por ejemplo, la existencia de una estructura equivalente no diferenciable en esferas de gran dimension pareciera ser algo sorprendente, pero no se le ocurrió a nadie llamarlo hermoso, ni en ese entonces, ni ahora" (Rota 1977, p.172).
Este desacuerdo ejemplifica la naturaleza subjetiva de la Belleza Matemática y su conexión con resultados matemáticos: en este caso, no sólo la existencia de esferas exóticas, sino también la realización particular de éstas.


0 comentarios:
Publicar un comentario